Time in a timeless universe (part 2)

A discussion of Julian Barbour's work on the nature of time

In a previous blog, I explained why the idea that 'time flows' – i.e. the idea that the present moment flows from the past into the future – is not the only way to understand time's role in physics. In fact, this intuitive notion that time flows is a misconception, one that was introduced into the foundations of physics by Sir Isaac Newton via his Principia Mathematica, where he wrote that 

'absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external, and by another name is called duration.' 

With this, Newton meant that the 'flow of time' is not determined by the behaviour of anything physical. In Newton's view, time is like a stage on which events can unfold, but it is not itself altered by the occurrence of events – or by anything else that happens in the physical universe. 

Newton introduced the idea of absolute time because he must have deemed it necessary for formulating dynamical laws, which in modern physics are expressed as differential equations, using another of Newton's inventions – differential calculus. Such equations of motion have been enormously successful explanations of the behaviour of matter, and perhaps it is because of the success of Newton's theory of dynamics that absolute time often goes unquestioned. It is, after all, hard to imagine dynamical laws without time. Yet by relying on absolute time, Newton created a problem: if time is never affected by the behaviour of anything – if absolute time is like an ideal stage on which events unfold without time being affected by any such event – then in what sense is time physical? 

The problem with absolute time is that it is ethereal: absolute time is outside our universes. Yet, there is a much more physical view of time, namely time as represented by a physical clock and the change it undergoes – what I shall call clock time. This notion of time as change is one that Newton wanted to separate from absolute time, as he went on to write that

 '…relative, apparent, and common time, is some sensible and external (whether accurate or unequable) measure of duration by the means of motion, which is commonly used instead of true time; such as an hour, a day, a month, a year.'

Indeed, there are fundamental differences between these two conceptions of time. My favourite thought experiment that clarifies how clock time differs from absolute time is the following: imagine that all physical systems in the universe suddenly 'freeze' relative to absolute time and that this 'freeze' lasts 100 years. Nothing in the universe could detect the 'freeze' or its duration because those things that could detect it – namely clocks – are 'frozen' and hence unable to detect the passage of absolute time. So, after this 100-year-long 'freeze' has ended, nothing in the universe will contain a record of the 'freeze'; the universe is exactly as it would've been had the ‘freeze’ not happened. Yet Newton would insist that the 'freeze' really happened because of the reality of absolute time.

Or consider a related example. Does time flow in a stationary universe? In such a universe, there is no change, so like in the previous example, nothing in this universe can record the flow of time. There is nothing to distinguish one moment from the next.

Such considerations have led physicists and philosophers like Leibniz and Mach to reject Newton's idea of absolute time in favour of relational theories of time, in which time exists because physical systems change. Mach summarised the motivation of those theories by noting that 

'it is utterly beyond our power to measure the changes of things by time. Quite the contrary, time is an abstraction, at which we arrive by means of the change of things.'

A remarkable and beautiful example of a relational theory of time is due to Julian Barbour, a contemporary physicist who has shown that Newton's theory of gravity can be formulated without absolute time. Ironically, this implies that Newton's own theory made his reliance on absolute time unnecessary, which Barbour also notes in his breakthrough paper, The Nature of Time, where he writes,

'Indeed, Newton can be hoist by his own petard if we see what his marvelous laws actually tell us. '

Barbour solved the problem of time, as it appears in Newtonian gravity, as follows: he considered a model of a classical universe consisting of N point masses that interact solely via Newtonian gravity. He then showed that if given a series of unordered snapshots of the universe (see figure below), one can reorder them so that time and dynamics emerge from them again. Of course, ‘snapshots’ is a metaphor: what is meant by a ‘snapshot’ is the 3N positions of all the point masses in the 3-dimensional universe at a particular moment – or what I shall call the configuration of those masses. So put differently, given an unordered set of the continuous infinity of configurations that the N point masses trace out over their history, one can reorder the set so that the flow of time reappears.

This is a pictorial representation of a set of unordered configurations of a system of masses, interacting via Newtonian gravity. The labels above the configurations represent absolute time, and circles of varying sizes represent the particles to indicate that they have different masses. Note that Barbour’s model consists of point particles, which have no size – unlike the masses in these pictures. The arrows attached to each mass represent velocities. Remarkably, Barbour does not require the particles’ velocities to reorder the configurations.

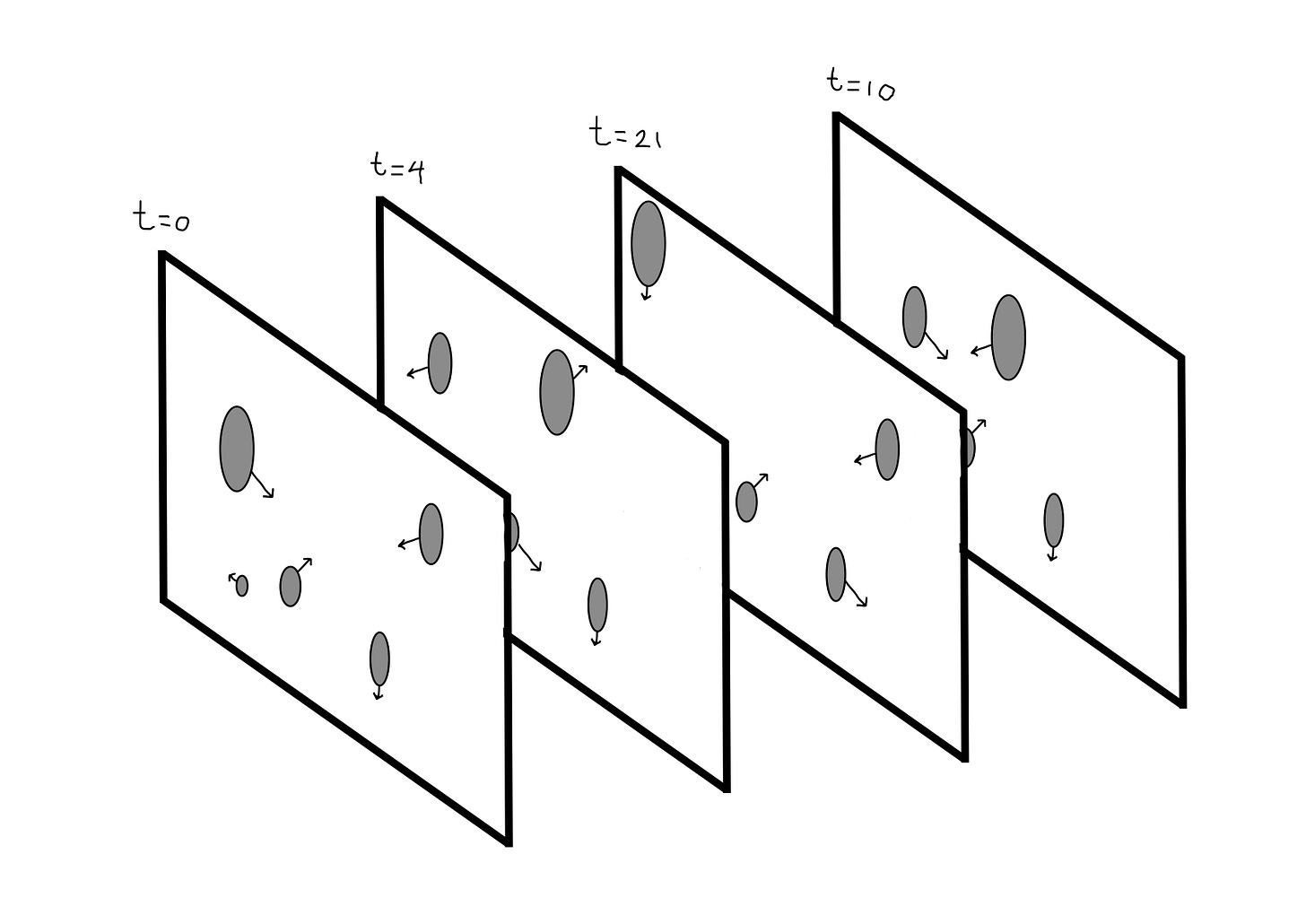
Barbour proved this by first showing that two configurations in the unordered set can be linked together through a procedure he calls best matching.¹ Roughly speaking, best matching takes two configurations and tells us whether the distances between the different positions of identical masses in those configurations have been minimised. Due to Newtonian mechanics, two sequential configurations are best matched, providing a way to reorder the set of unordered configurations (up to the direction of time). Barbour then demonstrated that the time interval between two best-matched configurations could be defined in terms of the masses' positions and the differences in position of identical masses between the two configurations. The exact expression for an infinitesimally small time interval, defined entirely in terms relative distances and energies, is given by

Here V and E are the potential and total energy of the N particles (E should be interpreted as a fundamental constant); mᵢ is the mass of the i’th particle; and 𝛿dᵢ is the displacement of the i’th particle between two best-matched configurations.

Consequently, the masses' positions are a clock because their configurations can be used to define time intervals, in terms of which Newton's laws can be formulated. That is to say that one can use 𝛿t to formulate the equations of motion of N particles. Barbour also demonstrates that there is precisely one trajectory in the configuration space of the N particles for which his definition of time emerges. Hence, one can derive Newton’s equations of motion by using completely timeless laws of physics.

Barbour's theory of time is a many-worlds theory because different times appear in his theory as different ‘worlds’ that coexist in a timeless block.² For instance, examine once more the figure above: the timeless approach shows us that we can rederive time from the unordered configurations if we take those configurations to be fundamental. Put differently, by positing the existence of a block of such unordered configurations, we get a theory of time for free. Moreover, if different times do not coexist in that way, they would have to come into existence relative to some external parameter, which would effectively be Newton's absolute time by another name.

Barbour's solution to the problem of time has a counterpart in quantum physics, known as the Page–Wootters construction, in which different times are exactly other universes in the Everettian sense (i.e. they are other universes in the sense of quantum theory’s many-worlds interpretation). I have written a paper on the Page–Wootters construction (it is open access and can be found here) and hope to write about it in a future post.

1. Barbour has a rigorous mathematical derivation of this result in Mach’s principle and the structure of dynamical theories, which can be found on his website. A more accessible explanation can be found in his book The End of Time.

2. It is unclear to me to what extent Barbour endorses the idea that different times are different universes, but it is what his model says about the world.